🧠 Matemática vetorial básica
Descubra o que são vetores e como usá-los na matemática e na física, com explicações simples e visuais divertidos para crianças em idade escolar.
Os vetores são ferramentas muito úteis na física e na matemática. Eles mostram não apenas quanto algo mede, mas também em que direção se move. Vamos aprender como somar e subtrair vetores com exemplos fáceis e visualizações divertidas.
⚙️ 1. O que é um vetor?
Um vetor tem duas partes importantes:
-
✅ Uma magnitude (valor numérico)
-
✅ Uma direção
Ele é representado por uma seta, com:
-
Uma cauda (início)
-
Uma ponta (final)
O tamanho da seta mostra o valor do vetor: quanto maior, maior a magnitude.
📘 Vetores são escritos com letras em negrito, como a ou b.
Se falamos só do tamanho, usamos barras: ||a||
➕ 2. Soma de vetores (mesma direção)
Quando somamos dois vetores, obtemos o vetor resultante.
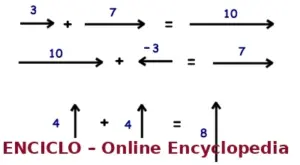
👀 Exemplos:
-
Vetor 3 + vetor 7 → Resultado = 10
-
Vetor 10 + vetor (−3) → Resultado = 7
-
Vetor 4 para cima + vetor 4 para cima → Resultado = 8 para cima
🧭 3. E quando os vetores estão em direções diferentes?
Quando os vetores têm direções diferentes, não podemos simplesmente somar os números. Nesse caso, usamos um método especial:
➡️ Método da cauda à ponta (Head-to-Tail)
Esse método funciona assim:
-
Desenhe o primeiro vetor
-
Coloque a cauda do segundo vetor na ponta do primeiro
-
Desenhe o vetor resultante da cauda do primeiro até a ponta do último
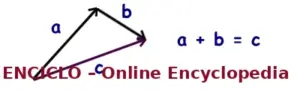
Funciona para dois ou mais vetores em qualquer ângulo.
📐 4. Usando o Teorema de Pitágoras
Se os dois vetores formam um ângulo de 90°, podemos usar o Teorema de Pitágoras para encontrar a magnitude do vetor resultante.
✏️ Exemplo:
João caminha 4 quilômetros para o norte e depois 3 quilômetros para o leste. Qual seria a distância se ele tivesse andado em linha reta?
Usamos a fórmula:
➡️ João teria andado 5 quilômetros em linha reta.
🔄 5. Lei comutativa
A lei comutativa diz que a ordem da soma dos vetores não altera o resultado.
a + b = b + a
🔁 6. Lei associativa
A lei associativa diz que, ao somar 3 ou mais vetores, não importa quais somamos primeiro.
(a + b) + d = a + (b + d)
Isso ajuda a organizar cálculos com vários vetores.
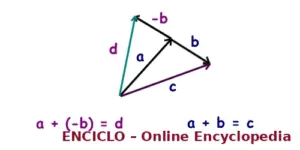
➖ 7. Subtração de vetores
Subtrair vetores é o mesmo que somar o vetor oposto:
a − b = a + (−b)
O vetor negativo tem a mesma magnitude do positivo, mas aponta para a direção contrária.
📚 Resumo para crianças curiosas
| Conceito | Explicação simples |
|---|---|
| Vetor | Tem direção e magnitude; desenhado como uma seta |
| Soma de vetores | Coloca um na ponta do outro e desenha o resultado |
| Teorema de Pitágoras | Usado quando vetores formam ângulo reto |
| Comutativa | a + b = b + a |
| Associativa | (a + b) + d = a + (b + d) |
| Subtração de vetores | Igual a somar com o oposto: a + (−b) |