🧠 Matemáticas vectoriales básicas
Aprende qué son los vectores y cómo se usan en matemáticas y física, explicado de forma clara y divertida para niños escolares. Ideal para aprender jugando.
Los vectores son una herramienta muy útil en la física y las matemáticas. Sirven para mostrar no solo cuánto mide algo (como la distancia o la velocidad), sino también en qué dirección va. Vamos a aprender cómo se suman y se restan los vectores con ejemplos simples y dibujos.
⚙️ 1. ¿Qué es un vector?
Un vector es una magnitud que tiene:
-
✅ Una magnitud (valor numérico)
-
✅ Una dirección
Los vectores se representan como una flecha, que tiene:
-
Una cola (inicio)
-
Una punta (final)
La longitud de la flecha representa la magnitud. Cuanto más larga, mayor es la cantidad.
📘 Se escriben con letras en negrita, como a o b.
Si solo hablamos de su tamaño, lo escribimos así: ||a||
➕ 2. Suma de vectores (misma dirección)
Cuando sumamos dos vectores, se obtiene el vector resultante.
👀 Ejemplos:
-
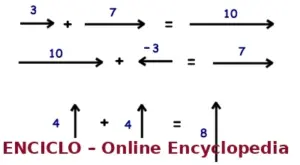
Si un vector mide 3 y otro 7 en la misma dirección → Resultado = 10
-
Si sumamos un vector de 10 con otro de −3 (en dirección opuesta) → Resultado = 7
-
Si sumamos 4 hacia arriba y 4 hacia arriba → Resultado = 8 hacia arriba
🧭 3. ¿Qué pasa si no están en la misma dirección?
Cuando los vectores apuntan en diferentes direcciones, no podemos sumarlos directamente. En ese caso usamos:
➡️ Método de punta a cola (Head-to-Tail)
Este método consiste en:
-
Dibujar el primer vector
-
Colocar el inicio del segundo vector justo en la punta del primero
-
Dibujar el vector resultante desde la cola del primero hasta la punta del último
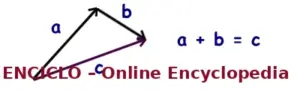
Este método funciona para cualquier número de vectores, incluso en diferentes ángulos.
📐 4. Usar el Teorema de Pitágoras
Si los vectores forman un ángulo de 90°, podemos usar el Teorema de Pitágoras para hallar el vector resultante.
✏️ Ejemplo:
Jim camina 4 millas al norte y luego 3 millas al este. ¿Cuánto habría caminado si fuera en línea recta desde el inicio hasta el final?
Usamos:
➡️ Jim habría caminado 5 millas en línea recta.
🔄 5. Ley conmutativa
La ley conmutativa dice que el orden en que sumamos vectores no cambia el resultado.
a + b = b + a
🔁 6. Ley asociativa
La ley asociativa dice que si sumamos 3 o más vectores, no importa cuáles sumamos primero.
(a + b) + d = a + (b + d)
Esto hace que trabajar con varios vectores sea más fácil y flexible.
➖ 7. Resta de vectores
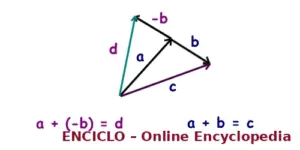
Restar un vector es lo mismo que sumarlo con su opuesto:
a − b = a + (−b)
El vector negativo tiene la misma magnitud que el positivo, pero apunta en dirección contraria.
📚 Resumen para niños escolares
| Concepto | Explicación sencilla |
|---|---|
| Vector | Tiene dirección y magnitud, se representa con una flecha |
| Suma de vectores | Une punta con cola y dibuja el vector resultante |
| Teorema Pitágoras | Sirve si los vectores forman ángulo recto |
| Conmutativa | a + b = b + a |
| Asociativa | (a + b) + d = a + (b + d) |
| Resta de vectores | Es igual a sumar con el opuesto: a + (−b) |